Special Points in Triangles

Which among the following is the point of intersection of the medians of a triangle?

The points $\mathrm{A}(–1, 4), \mathrm{B}(5, 2)$ are the vertices of a triangle of which$\mathrm{O}(0,–3)$ is centroid, then the third vertex C is_____.

Let $PS$ be the median of the triangle with vertices $P\left(2,2\right),Q\left(6,-1\right)$ and $R\left(7,3\right)$. The equation of the line passing through $\left(1,-1\right)$ and parallel to $PS$ is

A triangle has angles $90°,60°$ and $30°$. The orthocentre of the triangle will lie on the _____  of the triangle.

A triangle has angles $110°,30°$ and $40°$. The orthocentre of the triangle will lie _____ the triangle.

A triangle has angles $50°,60°$ and $80°$. The orthocentre of the triangle will lie _____ the triangle.

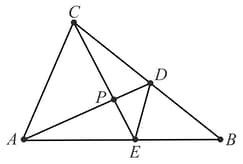
In $∆ABC,$ medians $\overline{AD}$ and $\overline{CE}$ intersect at $P, PE=1.5, PD=2$ and $DE=2.5$. What is the area of $2\left[AEDC\right]$?

If $A(5,2), B(10,12)$ and$P(x,y)$ are such that $\frac{AP}{PB}=\frac{3}{2}$, then the internal bisector of $\angle APB$ always passes through

Orthocentre of the triangle formed by the lines $x+y=1$ and $xy=0$ is

If $G\left(\overrightarrow{g}\right),H\left(\overrightarrow{h}\right)$ and $P\left(\overrightarrow{p}\right)$ are centroid, orthocenter and circumcenter of a triangle and $x\overrightarrow{p}+y\overrightarrow{h}+z\overrightarrow{g}=0$ then $\left(x, y, z\right)=$

The incentre of the triangle with vertices $\left(1\text{,}\sqrt{3}\right)$ , $(0,0)$ and $(2,0)$ is

The orthocentre of the triangle with vertices $\left(6,-1\right),\mathrm{ }\left(-2,-1\right)$ and $\left(2,5\right)$ is

The orthocentre of the triangle with vertices $\left(-2,-6\right),\mathrm{ }\left(-2,4\right)$ and $\left(1,3\right)$ is

If $G$ is the centroid of a $△ABC$ and $P$ is any other point in the plane, then $P{A}^2+P{B}^2+P{C}^2$ is equal to

The point that is equidistant from the vertices of the triangle is called

If the orthocentre and the centroid of a triangle are $(-3,5,2)$ and $(3,3,4)$ respectively, then its circumcentre is

The equation of the line joining the centroid with the orthocentre of the triangle formed by the points $\left(-2, 3\right), \left(2,-1\right), \left(4,0\right)$ is

The point of intersection of the line segment connecting the midpoints of two sides of a triangle is called

In an isosceles $△ABC, AB=AC$ and $D$ is midpoint of $BC$. Prove that circumcentre, in centre, orthocentre and centroid all are collinear.